W artykule przedstawiono dwa przykłady zastosowania zasad wyznaczania minimalnego zbrojenia ze względu na zarysowanie.
W artykule w [2] omówiono teoretyczne podstawy i znormalizowane zasady wyznaczania minimalnego zbrojenia ze względu na zarysowanie (mincr) z uwzględnieniem uzupełnień niemieckich [N2]. W publikacji [1] znajduje się wiele przykładów zastosowania tych zasad. Wśród nich siedem dotyczy zjawiska osiowego lub w przybliżeniu osiowego rozciągania, a w szczególności wpływu odkształceń termiczno-skurczowych (TS) na zarysowanie w:
■ wydzielonym elemencie osiowo rozciąganym
■ płycie stropowej
■ płycie fundamentowej
■ ścianie oporowej
■ ścianie wielokondygnacyjnego budynku podpiwniczonego
■ ścianie zbiornika prostokątnego.
W krótkim artykule nie da się przedstawić wielu przykładów, a zatem wybrano dwa:
■ element osiowo rozciągany, który może być realnym prętem albo może być prętem wyimaginowanym, reprezentującym rozciąganą część większej konstrukcji
■ płytę stropową.
Pierwszy z przykładów ilustruje zasady stosowania normy [N1] z uzupełnieniami niemieckimi [N2] w przypadku, w którym siła rozciągająca jest znana i zgodnie z [N1] jest równa sile rysującej. Drugi dotyczy zagadnienia, w którym miarodajna siła może być wynikiem obliczeń statycznych.
W obliczeniach stosuje się arkusze kalkulacyjne nr 3 i 4 dołączone do [1]. Arkusz nr 3 służy do obliczania szerokości rys w elementach rozciąganych z małym mimośrodem – wzory zastosowane do tego celu są zgodne z ogólną teorią zawartą w normie [N1]. Arkusz nr 4 służy do wyznaczania rozkładu temperatur w przekroju sposobem opisanym w [3] oraz do obliczania współczynnika pełzania i swobodnego skurczu betonu w funkcji czasu.
Przykład 1. Zarysowanie elementu osiowo rozciąganego
Oblicza się zbrojenie potrzebne do ograniczenia szerokości rys, mogących powstać pod wpływem skurczu betonu i odpływu ciepła hydratacji w osiowo rozciąganym elemencie (np. wyciętym ze ściany), który nie może się swobodnie odkształcać. Przykład ilustruje zastosowanie metod poziomu 0. Zbrojenie wyznaczono dwoma sposobami (skrócone nazwy metod zdefiniowano w [1] i [2]):
1) metodą Eu0, czyli ściśle według tekstu normy [N1] w dwóch wariantach:
1a) ze współczynnikiem k wyznaczonym na podstawie [N1]
1b) ze współczynnikiem k wyznaczonym z uwzględnieniem czwartego uzupełnienia niemieckiego
2) metodą Eu0n, czyli według [N1] z zastosowaniem drugiego uzupełnienia niemieckiego.
Jeżeli – jak się oczekuje – zarysowanie nastąpi w młodym betonie, to zakłada się, że w chwili zarysowania wytrzymałość na rozciąganie wynosi ƒct,eƒƒ = 0,5ƒctm, a jeżeli zarysowanie pojawi się w elemencie dojrzałym, to ƒct,eƒƒ = ƒctm.
Rozpatruje się ściany o grubościach 20, 30, 50 i 70 cm. Przyjęto: beton C 30/37, Ecm = 32,8 GPa, ƒctm = 2,9 MPa, c1 = c2 = 35 mm, wmax = 0,3 mm. W celu porównania wyników przyjęto, że zbrojenie składa się z prętów o średnicy 12 mm, nawet jeżeli rozstaw prętów jest bardzo mały. Przyjęto, że zarysowanie spowodowane odpływem ciepła hydratacji można uznać za obciążenie krótkotrwałe, czyli kt = 0,6.
Dalej przedstawiono przykład pełnego obliczenia dla ścian o grubościach 20 cm i 70 cm. Wyniki wszystkich obliczeń zestawiono w tabeli.
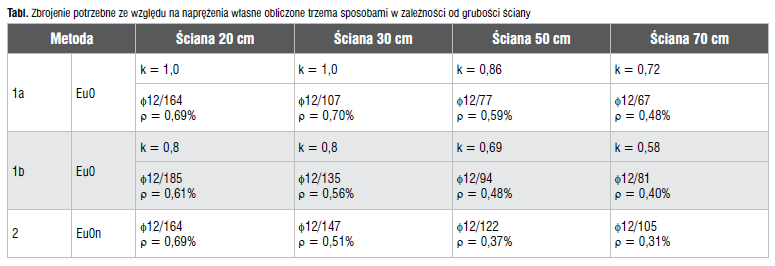
Metoda Eu0, współczynnik k wg [N1]
Ściana o grubości 20 cm
ƒct,eƒƒ = 0,5ƒctm = 0,5·2,9 = 1,45 MPa, k = 1,0 (element o grubości mniejszej niż 30 cm)
N = -kƒct,eƒƒAc = kƒct,eƒƒbh = -1,0·1,45·0,20·1,00·103 = -290,0 kN
Z arkusza nr 3 z [3] otrzymuje się φ12/164 z każdej strony, σs = -210 MPa, wk1 = wk2 = 0,299 mm < wmax = 0,3 mm, ρ = 0,69%, czyli około 0,35% po każdej stronie ściany.
Ściana o grubości 70 cm
ƒct,eƒƒ = 0,5ƒctm = 0,5·2,9 = 1,45 MPa, k = 0,72 (element o grubości większej od 30 cm i mniejszej od 80 cm)
N = -kƒct,eƒƒAc = -kƒct,eƒƒbh = -0,72·1,45·0,70·1,00·103 = -740,9 kN
Z arkusza nr 3 z [1] otrzymuje się φ12/67 z każdej strony, σs = -219,5 MPa, wk1 = wk2 = 0,296 mm < wmax = 0,3 mm, ρ = 0,48%.
Metoda Eu0, współczynnik k wg [N2] czwartego uzupełnienia niemieckiego
Ściana o grubości 20 cm
k = 0,8 (rys. 2 z [2])
N = -kƒct,eƒƒAc = -kƒct,eƒƒbh = -0,8·1,45·0,20·1,00·103 = -232,0 kN
Otrzymuje się φ12/185 z każdej strony, σs = -189,7 MPa, wk1 = wk2 = 0,298 mm < wmax = 0,3 mm, ρ = 0,61%, czyli około 0,30% po każdej stronie.
Ściana o grubości 70 cm
k = 0,58 (rys. 2 z [2])
N = -kƒct,eƒƒAc = -kƒct,eƒƒbh = -0,58·1,45·0,70·1,00·103 = -588,7 kN
Otrzymuje się φ12/81 z każdej strony, σs = –210,8 MPa, wk1 = wk2 = 0,296 mm < wmax = 0,3 mm, ρ = 0,40%.
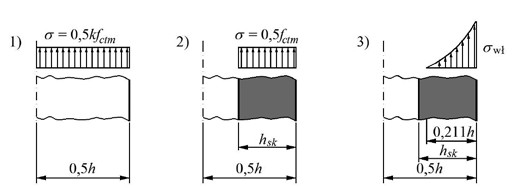 |
| Rys. 1. Ilustracja zasad obliczania zestawionych w tabeli |
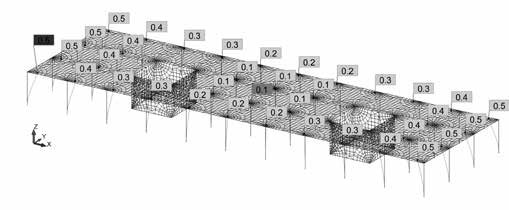 |
| Rys. 2. Podział na elementy skończone i przemieszczenia słupów [cm] |
Metoda Eu0n
Ściana o grubości 20 cm
a1 = 35 + 6 = 41 mm
Korzystając ze wzoru (2) wg [2] lub z wykresu na rys. 1 w [2], wyznacza się:
5a1 = 5·41 = 205 mm > h = 200 mm
2hsk = 5a1 = 5·41 = 205 mm > h = 200 mm
N = -ƒct,eƒƒbh = -0,5ƒctmbh = -0,5·2,90·1,00·0,20·103 = -290 kN
Dla wmax = 0,3 mm z arkusza nr 3 w [1] otrzymuje się φ12/164 z każdej strony, σs = -210,3 MPa, As = 13,79 cm2 > kƒct,eƒƒAc/ƒyk = 0,8·1,45·100·20/500 = 4,64 cm2,
ρ = 0,69%, czyli około 0,35% po każdej stronie.
Ściana o grubości 70 cm
a1= 35 + 6 = 41 mm
Korzystając ze wzoru (2) wg [2] lub z wykresu na rys. w [2], wyznacza się:
5a1 = 5·41 = 205 mm < h = 700 mm
2hsk = 4a1 + 0,2h = 4·41 + 0,2·700 = 304 mm
N = -ƒct,eƒƒb2hsk = -0,5ƒctmb2hsk = -0,5·2,90·1,00·0,304·103 = -440,8 kN
Dla wmax = 0,3 mm otrzymuje się φ12/105 mm z każdej strony, σs = -204,6 MPa, As = 21,54 cm2 > kƒct,eƒƒAc/ƒyk = 0,58·1,45·100·70/500 = 11,77 cm2,
ρ = 0,31%, czyli około 0,16% po każdej stronie.
W ścianie o grubości 20 cm pole skuteczne jest równe całemu polu przekroju betonu. Stosując drugie uzupełnienie niemieckie (wiersz 2 tab.), otrzymuje się więcej zbrojenia niż stosując normę [N1] z czwartym uzupełnieniem niemieckim (wiersz 1b), gdyż przyjmuje się średnie naprężenie rozciągające ƒct,eƒƒ = 0,5ƒctm, a nie 0,5kƒctm. W grubszych ścianach pole skuteczne jest mniejsze od całego pola przekroju betonu, w związku z tym zastosowanie drugiego uzupełnienia niemieckiego powoduje zmniejszenie wymaganego zbrojenia.
Przykład 2. Zarysowanie płyty stropowej pod wpływem sił podłużnych wywołanych odkształceniami termiczno-skurczowymi
W przykładzie zilustrowano zastosowanie arkuszy kalkulacyjnych z [1] do sprawdzania, czy zbrojenie w stropie płaskim jest wystarczające ze względu na skurcz i odpływ ciepła hydratacji. Rozpatrzono strop oparty na słupach i trzonach. Zastosowano metody Eu0, Eu0n i Eu1. Przeprowadzono analizę wpływu przerw roboczych na zbrojenie mincr.
Rozpatruje się płytę stropową o grubości 30 cm, długości 10x6 m = 60 m i szerokości 3x6 m = 18 m. Wysokość słupów 4,5 m, przekrój poprzeczny 40x40 cm, grubość ścian trzonów 20 cm.
Ewentualne rysy spowodowane naprężeniami TS mogą przekroczyć szerokość graniczną przede wszystkim w tych obszarach, w których zbrojenie zaprojektowane ze względu na nośność jest najmniejsze. Założono, że na całej powierzchni płyty zastosowano „podstawową” siatkę zbrojenia φ12/150 górą i dołem (oczywiście ze względu na obciążenia bezpośrednie dolne zbrojenie w środku przęseł i górne zbrojenie nad podporami będzie silniejsze od „podstawowego”).
Obliczając szerokość rys w pierwszym terminie krytycznym (terminie 1), bierze się pod uwagę tylko „podstawową” siatkę zbrojenia. Na końcu przykładu umieszczono także uwagi dotyczące płyt bez zbrojenia górą w obszarach, w których w drugim terminie krytycznym zawsze występuje ściskanie.
Beton C 30/37, Ecm = 32,8 GPa, ƒctm = 2,90 MPa, współczynnik Poissona ν = 0,2, współczynnik rozszerzalności termicznej betonu αt = 10–5, stal ƒyk = 500 MPa, Es = 200 GPa, pręty φ12 mm, otulenie zbrojenia głównego c = 43 mm, dopuszczalna szerokość rys wmax = 0,4 mm, b = 100 cm, h = 30 cm, k1 = 0,8, kt = 0,6 w terminie 1, kt = 0,4 w terminie 2. Rozstaw prętów w obszarach rozciąganych nie powinien przekraczać 5(c + 0,5φ) = 5(43 + 0,5·12) = 245 mm.
Według rozdziału 9 normy [N1] maksymalny rozstaw zbrojenia w płycie o grubości 30 cm wynosi 400 mm, a gdy uznamy rozpatrywane zbrojenie za drugorzędne, to nawet 450 mm. Jeżeli jednak zbrojenie jest uwzględniane w obliczeniach szerokości rys, a rozstaw prętów przekracza 5(c + 0,5φ), to zgodnie z pkt 7.3.4(3) normy [N1] podstawowy wzór (7.11) określający sr,max przestaje być ważny. Górną granicę szerokości rys można wtedy obliczyć ze wzoru sr,max = 1,3(h – x), ale w pierwszym terminie krytycznym płyta jest osiowo rozciągana, x = 0 i nie wiadomo, czy ta zasada normy ma wtedy sens. W związku z tym w obszarach narażonych na zarysowanie nie stosowano rozstawów większych niż 5(c + 0,5φ).
Metoda Eu0
Zbrojenie mincr wyznacza się dla M = 0, N = Ncr, współczynnik k = 0,80 (rys. 2 z [2])
![]()
Dla podstawowej siatki zbrojenia φ12/150 z arkusza nr 3 (dla kt = 0,6) otrzymano wk = 0,373 mm < wmax = 0,4 mm.
Metoda Eu0n
Ze wzoru (2) z [2] lub z rys. 1 z [2] odczytano hsk = 12,8 cm.
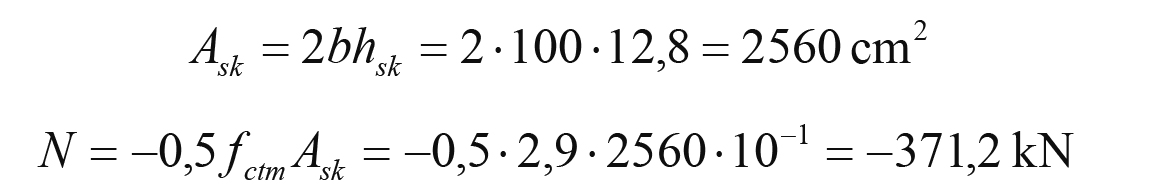
Otrzymano wk = 0,403 mm ≅ wmax = 0,4 mm.
Wniosek. Ze względu na naprężenia działające w terminie 1 wystarczające jest zbrojenie φ12/150 przy każdej powierzchni (przy każdej powierzchni stopień zbrojenia wynosi około 0,25%). Jak widać, zastosowanie drugiego uzupełnienia niemieckiego do obliczania płyty o grubości 30 cm nie przyniosło korzyści. Rozstaw ewentualnych przerw roboczych i dylatacji stałych nie ma wpływu na obliczenia na poziomie 0.
Metoda Eu1
Naprężenia wymuszone, które mogą mieć znaczący wpływ na wymagane zbrojenie, zależą od schematu statycznego i rozmieszczenia przerw roboczych.
Naprężenia własne wyznaczono, stosując arkusz nr 4 z [1]
Naprężenia wymuszone obliczono metodą elementów skończonych, stosując program Autodesk Robot Structural Analysis 2017 [4]. Płytę stropową zamodelowano prostokątnymi elementami powłokowymi, a słupy elementami belkowymi. Założono, że dolne końce słupów są utwierdzone. Przyjęto, że moduł sprężystości betonu wynosi Ec = 0,9Ecm = 29,5 GPa. W obliczeniach liniowo sprężystych nie uwzględnia się zarysowania konstrukcji, w związku z tym w modelu mogą się pojawić naprężenia większe od naprężenia rysującego. W rzeczywistości jednak naprężenia w betonie w obszarach, w których przekroczono wytrzymałość na rozciąganie, spadną i zbrojenie obliczone na siłę rysującą będzie wystarczające.
Przyjęto, że w terminie 1 strop leży na deskowaniu, a odpływ ciepła hydratacji wywołuje w nim tylko osiowe rozciągania lub ściskania spowodowane brakiem swobody odkształceń w płaszczyźnie stropu. W związku z tym w obliczeniach MES założono, że jedyne obciążenie płyty stanowi równomierny spadek temperatury.
Przy równomiernym skurczu betonu niesymetryczne zbrojenie (górna warstwa zbrojenia nie jest taka sama jak dolna) może być powodem zakrzywienia stropu, czyli strop może mieć tendencję do „wstawania” z deskowania, na którym leży. Założono, że ciężar własny prostuje ewentualne zakrzywienia i można rozpatrywać strop jako prosty, osiowo rozciągany lub ściskany.
Wpływ odkształceń TS analizowano, przyjmując, że skrócenie, które wystąpiłoby w płycie stropowej odłączonej od słupów i trzonów, jest jednakowe na całej powierzchni i równe swobodnemu skróceniu płyty.
Na podstawie obliczeń w arkuszu nr 4 z [1] (obliczeń tych nie przedstawiono) przyjęto, że różnica temperatury jest równa 19,5oC.
 |
| Rys. 3. Wymuszone naprężenia normalne σx (rozciąganie dodatnie) |
Płyta oparta na słupach i trzonach, wykonana bez przerw roboczych
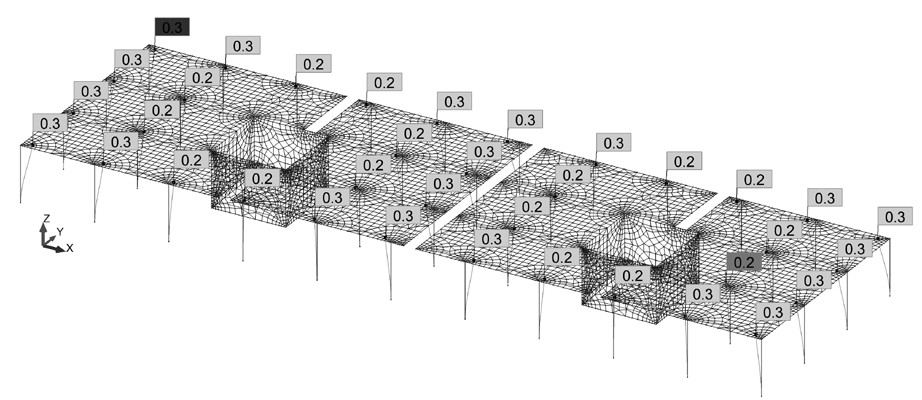
Założono, że płytę stropową opartą na słupach i dwóch trzonach wykonano w całości, bez stosowania przerw roboczych. Na rys. 2 przedstawiono podział na elementy skończone i przemieszczenia słupów, a na rys. 3 – plan warstwicowy naprężeń wymuszonych σx.
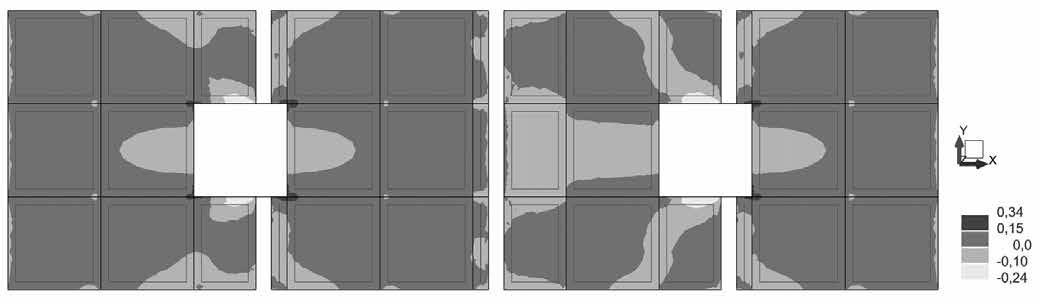
Na wykresie warstwicowym naprężeń wyróżniono trzy obszary: biały, jasnoszary i ciemnoszary.
Obszar biały – suma własnych i wymuszonych naprężeń rozciągających przekracza ƒct,eƒƒ
σwł + σwym > 0,5ƒctm czyli σwym > 0,5ƒctm – σwł = 0,5·2,9 – 0,47 = 0,98 MPa.
Zbrojenie w tym obszarze należy sprawdzić tak jak w obliczeniach na poziomie 0, a więc właściwe będzie zbrojenie φ12/150.
Obszar jasnoszary – występuje rozciąganie, ale
σwł + σwym ≤ 0,5ƒctm czyli σwym ≤ 0,5ƒctm – σwł = 0,98 MPa.
W tym obszarze, zgodnie z pierwszym uzupełnieniem niemieckim, można zaprojektować zbrojenie na siłę rozciągającą rzeczywiście występującą w płycie N = -Ac (σwym + 0,3σwł) (wyprowadzenie wzoru w [1]), lecz nie większą niż siła obliczona metodą Eu0 lub Eu0n. Obszar jasnoszary należy podzielić na podobszary. W każdym podobszarze zbrojenie oblicza się na podstawie największego naprężenia wymuszonego, które w nim występuje. Przykładowo dla naprężenia σwym = 0,40 MPa, miarodajna siła rozciągająca wynosi:![]()
Dla siatki podstawowej φ12/230 górą i dołem z arkusza nr 3 z [1] otrzymano szerokość rys wk = 0,384 mm < wmax = 0,4 mm.
Obszar ciemnoszary – występują tylko naprężenia ściskające.
Nie uwzględniając redukcji naprężeń własnych przez wymuszone naprężenia ściskające, można zwymiarować zbrojenie tylko ze względu na naprężenia własne, na siłę N = -0,3Acσwł
W obszarach dużych wymuszonych naprężeń ściskających suma naprężeń wymuszonych i własnych jest naprężeniem
ściskającym. W takim obszarze wystarczyłoby zastosować tylko zbrojenie konstrukcyjne. W omawianym przykładzie mamy:

Dla zbrojenia φ12/240 (ρ = 0,31%) na podstawie obliczeń
w arkuszu nr 3 otrzymano
wk = 0,108 mm ≤ wmax = 0,4 mm.
Dla zbrojenia φ10/ 240 (ρ = 0,22%), przy tym samym otuleniu c = 43 mm, otrzymano wk = 0,180 mm ≤ wmax = 0,4 mm.
Warto zauważyć, że ewentualne rysy powstałe od odpływu ciepła hydratacji przy słabiej zbrojonej powierzchni płyty mogą się zamknąć na skutek oddziaływań bezpośrednich, które wystąpią po usunięciu deskowania.
 |
| Rys. 4. Podział stropu przerwami roboczymi |
 |
| Rys. 5. Podział na elementy skończone i przemieszczenia słupów [cm] |
Płyta z przerwami roboczymi oparta na słupach i trzonach
Skutecznym sposobem zapobiegania zarysowaniu w terminie 1 jest stosowanie przerw roboczych. Założono, że rozmieszczono je zgodnie z zaleceniem normy [N1] co 15 m (rys. 4). Na rys. 5 przedstawiono podział na elementy skończone i przemieszczenia końców słupów, a na rys. 6 – plan warstwicowy naprężeń wymuszonych σx powstałych na skutek odpływu ciepła hydratacji.
Z rys. 6 odczytano, że największe naprężenie wymuszone w płycie wynosi σwym = 0,34 MPa, a suma naprężeń wynosi:![]()
W związku z tym zbrojenie mincr należy sprawdzić na siłę rozciągającą równą: ![]()
Dla siatki podstawowej φ12/240 górą i dołem (ρ = 0,31%) z arkusza nr 3 z [1] otrzymano szerokość rys wk = 0,370 mm < wmax = 0,4 mm.
Dla zbrojenia φ10/190 (ρ = 0,28%) otrzymano wk = 0,396 mm < wmax = 0,4 mm.
Analogiczne obliczenia można przeprowadzić dla naprężeń σy.
 |
| Rys. 6. Wymuszone naprężenia normalne σx (rozciąganie dodatnie) |
Komentarze i wnioski
Termin 1
Przedstawione w artykule modele są w znacznym stopniu uproszczone. Założono w nich, że:
■ beton jest materiałem liniowo sprężystym, a słupy są utwierdzone na dolnym końcu i nie ulegają zarysowaniu
■ pomija się wpływ deskowania oraz podpór tymczasowych (stempli) na zwiększenie sztywności tarczowej całego układu
■ nie uwzględnia się podatności połączenia płyta-słup.
W związku z tym można oczekiwać, że w rzeczywistości naprężenia wymuszone będą mniejsze niż obliczone.
Analiza metodami poziomu 0 prowadzi do stosunkowo gęstej podstawowej siatki zbrojenia φ12/150 górą i dołem na całej powierzchni płyty. Dylatacje i przerwy robocze nie wpływają na wynik analizy na tym poziomie.
Analiza na poziomie 1 doprowadza do korzystniejszych rozwiązań. W konstrukcji z elementami usztywniającymi (trzonami) w obszarach białych potrzebne jest zbrojenie φ12/150 górą i dołem, a w innych miejscach można zastosować mniejsze zbrojenie.
Jeżeli zastosuje się odpowiednio rozmieszczone przerwy robocze, to naprężenia rozciągające w terminie pierwszym będą bardzo małe, a potrzebne zbrojenie niewielkie. W związku z tym pojawia się pytanie dotyczące zbrojenia górą w obszarach, w których w drugim terminie krytycznym zawsze występuje ściskanie (zwykle w środkach przęseł). Czy można – jak to często robiono dawniej – nie stosować zbrojenia górą w tych obszarach? Tu trzeba zauważyć, że dawniej zazwyczaj stosowano cieńsze płyty i słabszy beton niż dzisiaj. Według normy [N1] w każdym obszarze, w którym może się pojawić rozciąganie, należy stosować zbrojenie minimalne. Jednakże w płytach ciągłych rysy, które mogą powstać na górnej powierzchni płyty w obszarach, o których tu mowa, zapewne zamkną się pod wpływem ściskania wywołanego przez obciążenia bezpośrednie. Dlatego uważamy, że pominięcie górnego zbrojenia w takich obszarach nie powinno być uznawane za błąd, pod warunkiem że zastosowano odpowiednio rozplanowane przerwy robocze i dylatacje redukujące do minimum rozciągające siły podłużne mogące powstać w drugim terminie krytycznym.
Warto jeszcze zwrócić uwagę na fakt, że analiza naprężeń TS umożliwia konstruktorowi wybór – kosztem powiększenia zbrojenia można zastosować mniej przerw roboczych, które przecież też pociągają za sobą koszty i niedogodności wykonawcze.
Termin 2
W terminie 2 strop jest rozszalowany, a tymczasowe podpory usunięte. Zwykle dominującymi siłami przekrojowymi są momenty zginające – pojawia się strefa ściskana, która ogranicza szerokość rys. W tym terminie zarysowanie może powstać pod łącznym wpływem obciążeń bezpośrednich i naprężeń wymuszonych. Zbrojenie mincr w terminie 2 oblicza się zgodnie z normą [N1] jako minimalne zbrojenie na zarysowanie przy zginaniu. Otrzymany w ten sposób stopień zbrojenia jest zbliżony (większy) do minimalnego zbrojenia ze względu na nośność, a dokładniejsze obliczenia mogą przynieść tylko niewielką korzyść.
W omawianym tu przykładzie mamy: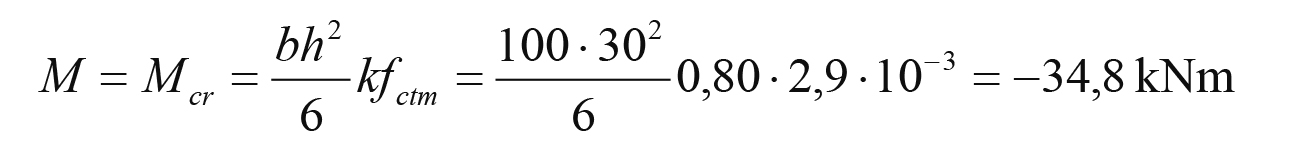
Dla tego momentu zginającego dla siatki podstawowej φ12/230 (ρ = 0,33%) otrzymano wk = 0,283 mm < wmax = 0,4 mm.
Nie należy całkowicie lekceważyć rozciągających sił podłużnych, które mogą powstać pod wpływem ograniczenia swobody skurczu betonu. Siły te nie mają praktycznie wpływu na nośność graniczną, gdyż przy dużych odkształceniach, które są wywołane przez inne obciążenia, sztywność stropu spada i wymuszone siły maleją, mogą mieć jednak wpływ na szerokość rys, gdy występują silne ograniczenia swobody odkształceń w płaszczyźnie stropu. Warto zauważyć, że jeżeli model MES ma służyć do wyznaczenia sił podłużnych, to trzeba stosować elementy powłokowe, gdyż elementy płytowe nie stwarzają takiej możliwości.
prof. dr hab. inż. Michał Knauff
Szkoła Główna Gospodarstwa Wiejskiego w Warszawie
mgr inż. Bartosz Grzeszykowski
dr inż. Agnieszka Golubińska
Politechnika Warszawska
Normy
N1. PN-EN 1992-1-1:2008/NA:2010 Eurokod 2 Projektowanie konstrukcji z betonu. Część 1-1: Reguły ogólne i reguły dla budynków.
N2. DIN EN 1992-1-1/NA Nationaler Anhang – National festgelegte Parameter – Eurocode 2: Bemessung und Konstruktion von Stahlbeton- und Spannbetontragwerken – Teil 1–1: Allgemeine Bemessungsregeln und Regeln für den Hochbau, 2011.
Literatura
1. Knauff M., Grzeszykowski B., Golubińska A., Przykłady obliczania konstrukcji żelbetowych, Zeszyt 3 „Zarysowanie”, PWN, Warszawa 2017.
2. Knauff M., Grzeszykowski B., Golubińska A., Wybrane problemy obliczania minimalnego zbrojenia wg PN-EN – zasady, „Inżynier Budownictwa” nr 5/2018.
3. Flaga K., Klemczak B., Konstrukcyjne i technologiczne aspekty naprężeń termiczno-skurczowych w masywnych i średniomasywnych konstrukcjach betonowych, Politechnika Krakowska, Seria „Inżynieria Lądowa”, monografia 521, Kraków 2016.
4. Autodesk Robot Structural Analysis Professional 2017.

ul. Chłodna 48, lok. 199
00-867 Warszawa
tel. 22 255 33 40
KRS 0000192270 (Sąd Rejonowy dla m.st. Warszawy, XII Wydział Gospodarczy KRS)
NIP 525-22-90-483
Kapitał zakładowy: 150 000 zł
Produkty (0)